牛顿逼近法可以很容易解决求近似值的问题.
经典的例子是: 如何通过加减乘除来进行开跟号计算.
原函数: f(x) = x^2
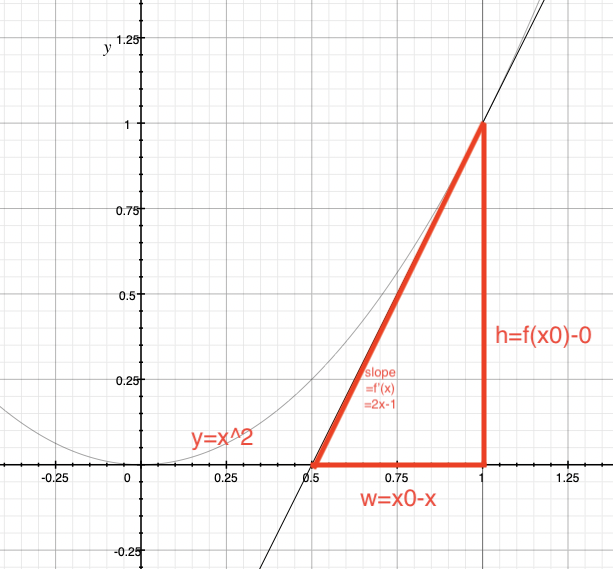
在函数图像上, 取 x0=1, 也就是点 (1, 1), 做 f(x) 在这个点的切线.
切线: f'(x) - 1 = 2(x-1), 即 f'(x) = 2x - 1.
在切点附近, f'(x) 的值比无限逼近 f(x), 利用切线与 x 轴形成的三角形, 我们可以得出:
f(x) / (x0 - x) = f'(x), 即 x0 - x = f(x) / f'(x).
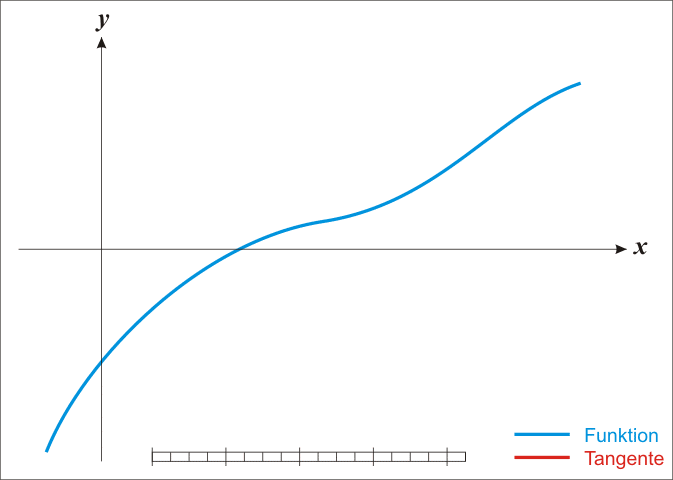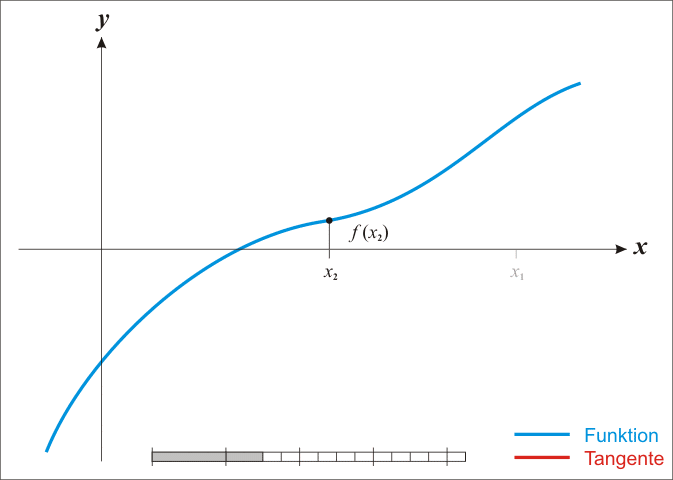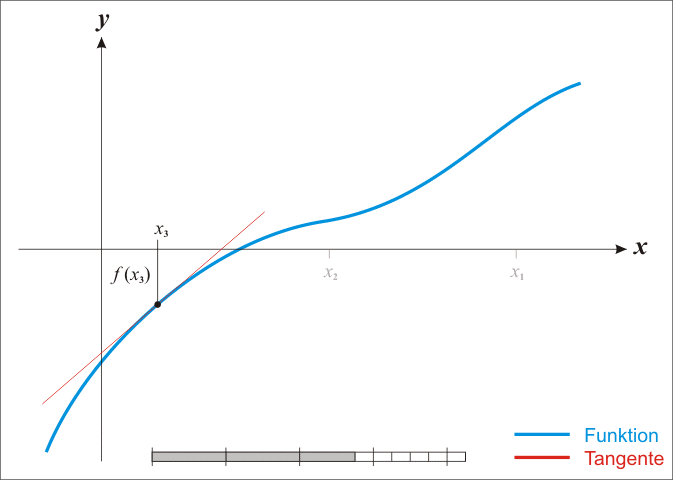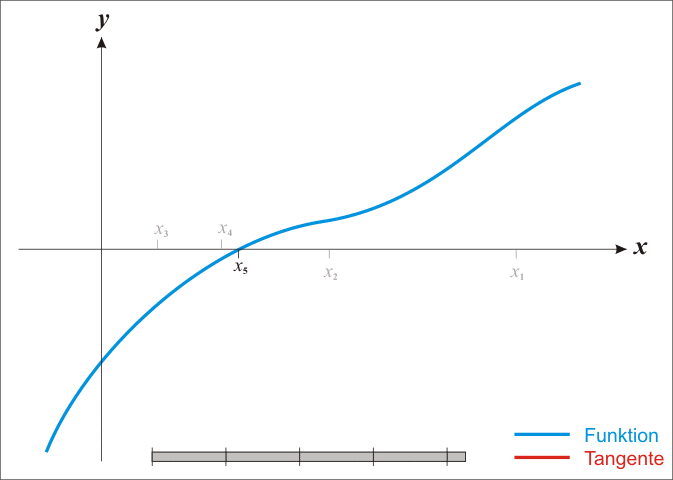
如 GIF 所示, 只要这样不停地逼近, 就能找到一个精度足够高的近似解.
转化为 golang 代码:
package main
import (
"fmt"
"math"
)
const PRECISION float64 = 0.0000000001
const START_SPECULATE = 1.0
func Sqrt(x float64) (float64, int) {
times := 0
z := START_SPECULATE
for !(math.Abs(x-z*z) <= PRECISION) {
z += -1 * (z*z - x) / (2 * z)
times += 1
}
return z, times
}
func main() {
var z float64
var t int
z, t = Sqrt(2)
fmt.Printf("Sqrt(2): %.9f\ttimes: %d\n", z, t)
z, t = Sqrt(9)
fmt.Printf("Sqrt(9): %.9f\ttimes: %d\n", z, t)
}
output:
Sqrt(2): 1.414213562 times: 4
Sqrt(9): 3.000000000 times: 6
START_SPECULATE 是我们迭代的起始坐标, 理论上来说可以随便取.
很显然, 更合理的初值会减小逼近计算的次数, 但是这又是另一个问题了~
参考
https://zh.wikipedia.org/zh-hans/%E7%89%9B%E9%A1%BF%E6%B3%95
https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E8%BF%AD%E4%BB%A3%E6%B3%95